快速排序 - ONESRC

快速排序（Quicksort）是对冒泡排序的一种改进，它使用了分治法（Divide and conquer）策略，把一个复杂的问题分成两个或更多的相同或相似的子问题，直到最后子问题可以简单的直接求解，原问题的解即子问题的解的合并。

排序思路

快速排序把一个序列（list）分为两个子序列（sub-lists）。

从数列中挑出一个元素，称为「基准」（pivot），
重新排序数列，所有比基准值小的元素摆放在基准前面，所有比基准值大的元素摆在基准后面（相同的数可以到任何一边）。在这个分割结束之后，该基准就处于数列的中间位置。这个称为分割（partition）操作。
递归地（recursively）把小于基准值元素的子数列和大于基准值元素的子数列排序。
递归到最底部时，数列的大小是零或一，也就是已经排序好了。这个演算法一定会结束，因为在每次的迭代（iteration）中，它至少会把一个元素摆到它最后的位置去。

递归模型如下：

$$ f(R,s,t) \begin{cases} nothing \qquad \text {R[s..t]中没有或者只有一个元素} \\ \\ do \begin{cases} i =partiton(R,s,t);\\f(R,s,i-1); \qquad \text {其他情况} \\f(R,i+1,t); \end{cases} \end{cases} $$

排序算法

以c为例,从小到大排序

#include<stdio.h>

int partition(int R[],int s,int t){
    int i=s,j=t;//这里取第一个元素为基准，你也可以取其他元素
    int tmp=R[i];
    while(i<j){
        while(i<j&&R[j]>=tmp)j--;//从右边取第一个比它小的元素，放到左边
        R[i]=R[j];
        while(i<j&&R[i]<=tmp)i++;//从左边取第一个比它大的元素，放到右边
        R[j]=R[i];
    }
    R[i]=tmp;//一次分割完成，右边的元素<=R[i]<=左边的元素，全局有序
    
    //打印结果
    int k;
    for (k = 0; k < 10;k++){
        printf("%d ",R[k]);
    }
    printf("\n");
    
    return i;
}
void quick_sort(int R[],int s,int t){
    int i;
    if(s<t){
        i=partition(R,s,t);
        quick_sort(R,s,i-1);
        quick_sort(R,i+1,t);
    }
}
int main(void){
    int a[] = {6,8,7,9,0,1,3,2,4,5};
    quick_sort(a,0,9);
}

输出结果：

5 4 2 3 0 1 6 9 7 8
1 4 2 3 0 5 6 9 7 8
0 1 2 3 4 5 6 9 7 8
0 1 2 3 4 5 6 9 7 8
0 1 2 3 4 5 6 9 7 8
0 1 2 3 4 5 6 8 7 9
0 1 2 3 4 5 6 7 8 9

过程分析

以 6 8 7 9 0 1 3 2 4 5 为例，

第一次划分 i=s=6 此时6已经被记录下来了，它的位置可以放置其他元素，我们用*表示。

* 8 7 9 0 1 3 2 4 5 从右边开始遍历，寻找第一个比6小的元素。找到5，将5放到6原来的位置。
5 8 7 9 0 1 3 2 4 * 从左边开始遍历，寻找第一个比6大的元素。找到8，将8放到5原来的位置。
5 * 7 9 0 1 3 2 4 8
......
5 4 2 3 0 1 * 9 7 8 直到i==j ，将tmp=6放回，一次分割完成。

原地分割版本：

#include<stdio.h>

int partition(int R[],int s,int t){
    int tmp=R[s];//这里选择s为基准，也可以选择其他元素
    R[s]=R[t];//这基准元素，放到最后一个位置
    R[t] = tmp;
    int i,index = s;//这里记录下分割位置
    for (i = s; i < t;i++){//从第一个遍历至倒数第二个,找到其位置
        if(R[i]<tmp){//tmp较大,tmp位置应该滞后
            int tmp2 = R[index];//交换index和当前元素
            R[index] = R[i];
            R[i] = tmp2;
           index++;//滞后
        }
    }
    int tmp2 = R[index];// 将基准元素放入
    R[index] = R[t];
    R[t] = tmp2;

    //打印结果
    int k;
    for (k = 0; k < 10;k++){
        printf("%d ",R[k]);
    }
    printf("\n");
    return index;
}
void quick_sort(int R[],int s,int t){
    int i;
    if(s<t){

        i=partition(R,s,t);
        quick_sort(R,s,i-1);
        quick_sort(R,i+1,t);
    }
}
int main(void){
    int a[] = {6,8,7,9,0,1,3,2,4,5};
    quick_sort(a,0,9);
}

动图示例：

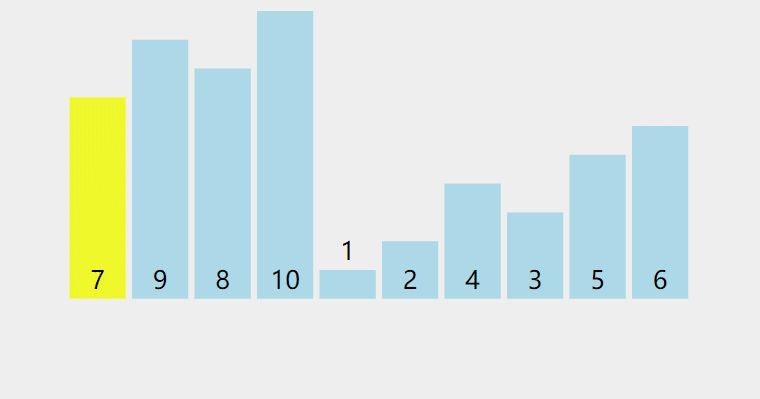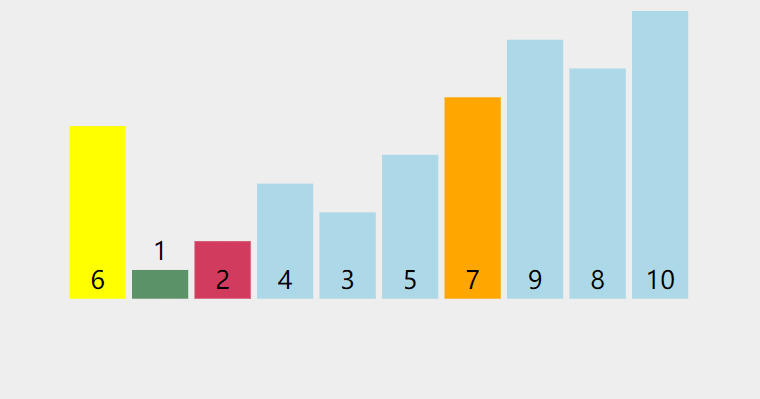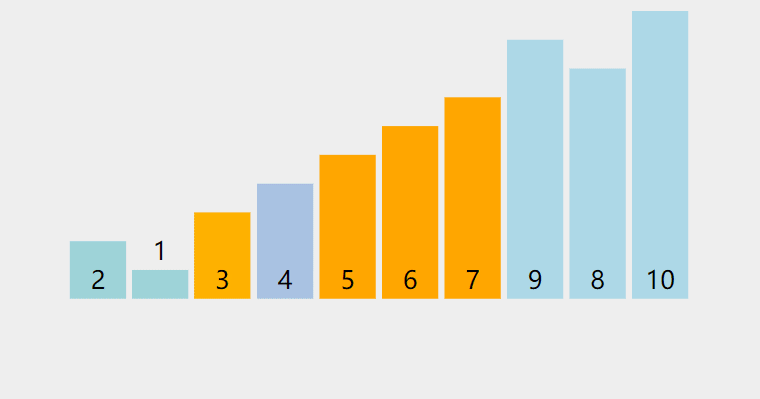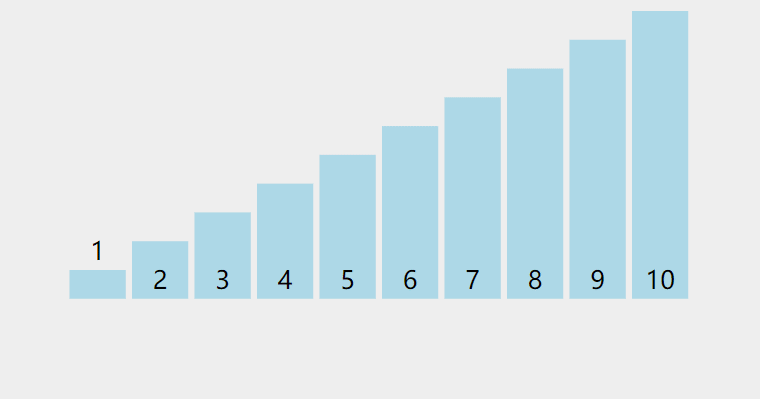
图片来自https://visualgo.net，它采用的是第二种方法

算法分析

时间复杂度、空间复杂度：

平均情况：

设执行时间为T，得到递归关系式：

$$ 执行时间 \quad T(n) = cn+\frac{1}{n}\sum_{k=1}^{n}(T(k-1)+T(n-k)) \qquad其中一次分割为线性时间，不妨设为cn $$

故时间复杂度为O(nlog2n)，空间复杂度为O(log~2~n)

最坏情况：递归树高度为n，每一层划分时间为n-1，所以时间复杂度为O(n^2^) ，空间复杂度为O(n)
最好情况：递归树高度为O(log~2~n)，每一层划分时间为O(n)，所以时间复杂度为O(nlog~2~n) ，空间复杂度为O(log~2~n)

初始数据正序或者反序时，呈现最坏情况；初始数据随机分布时呈现较好的情况

稳定性：

相同元素的相对位置可能发生改变，这是一种不稳定的排序方法。如{5，2，4，8，7，4}

复杂性：

较复杂

归位：

全局有序。

本文由 ukuq 创作，采用知识共享署名4.0 国际许可协议进行许可
本站文章除注明转载/出处外，均为本站原创或翻译，转载前请务必署名
最后编辑时间为: Jan 26, 2019 at 09:44 pm