冒泡排序 - ONESRC

交换排序的基本思想是两两比较待排序的元素，反序时进行交换，直至没有反序元素为止。冒泡排序是最简单的交换排序，也是很多人接触到的第一种排序算法。

排序思路

通过无序区相邻元素的比较，进行位置交换，使得最小的元素如气泡般逐渐往上“漂浮”直至“水面”，或者使得最大元素“沉到”最下面。

排序算法

以c为例,从小到大排序，采用最小元素漂浮。

#include<stdio.h>

void bubble_sort(int R[],int n){
    int tmp,i,j;
    for(i=0;i<n-1;i++){
        for(j=n-1;j>i;j--){//这里亦可以修改为for(j=0;j<n-1-i;j++),比较j和j+1，使得最大元素下沉。
            if(R[j]<R[j-1]){//交换R[j]与R[j-1]的顺序
                tmp = R[j];
                R[j]=R[j-1];
                R[j-1]=tmp;
            }
        }
        //打印第i趟排序后的结果
        printf("%d: ",i);
        int k;
        for (k = 0; k < n;k++){
            printf("%d ", R[k]);
        }
        printf("\n");
    }
}
int main(void){
    int a[] = {9,8,7,6,5,4,3,2,1,0};
    bubble_sort(a, 10);
}

动图演示：

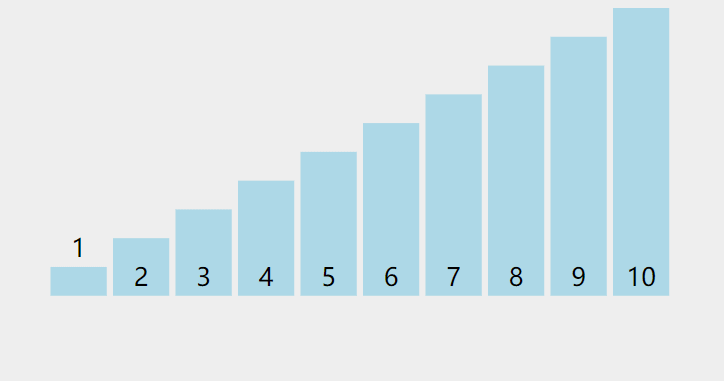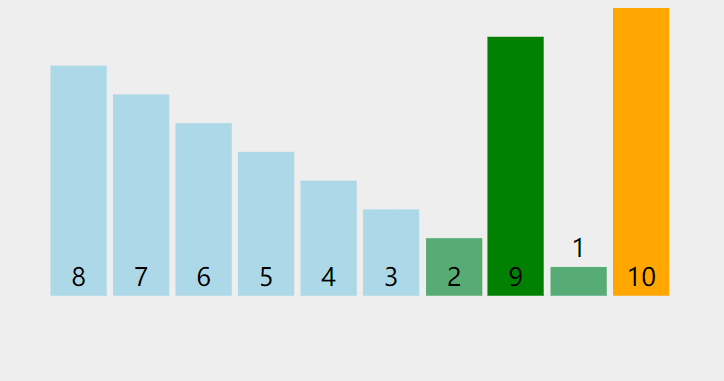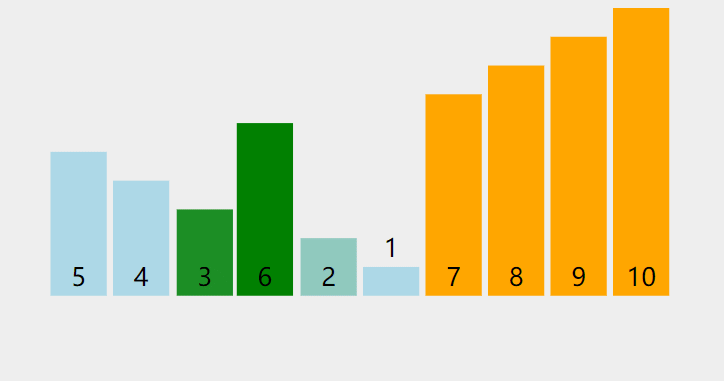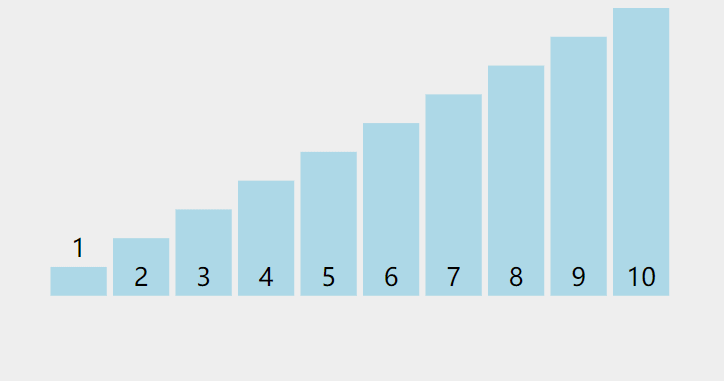
注：图片来自https://visualgo.net，它采用的是下沉的方法，个人觉得上浮的更好一些。

输出结果：

0: 0 9 8 7 6 5 4 3 2 1
1: 0 1 9 8 7 6 5 4 3 2
2: 0 1 2 9 8 7 6 5 4 3
3: 0 1 2 3 9 8 7 6 5 4
4: 0 1 2 3 4 9 8 7 6 5
5: 0 1 2 3 4 5 9 8 7 6
6: 0 1 2 3 4 5 6 9 8 7
7: 0 1 2 3 4 5 6 7 9 8
8: 0 1 2 3 4 5 6 7 8 9

算法优化：

如果在某一趟中未出现交换，则说明已经排好序了，不必再进行后面的循环了

#include<stdio.h>
#include<stdlib.h>
void bubble_sort1(int R[],int n){
    int tmp,i,j;
    //　在C语言标准(C89)没有定义布尔类型(现在一般用C99)，所以C语言判断真假时以0为假，非0为真。这里用int型代替bool了
    int exchange;//记录是否发生了交换
    for(i=0;i<n-1;i++){
        exchange=0;//初始化为0
        for(j=n-1;j>i;j--){
            if(R[j]<R[j-1]){//交换R[j]与R[j-1]的顺序
                tmp = R[j];
                R[j]=R[j-1];
                R[j-1]=tmp;
                exchange=1;//发生交换，置1
            }
        }
        if(exchange==0)return;//未发生交换，说明已排好序，返回即可
        //打印第i趟排序后的结果
        printf("%d: ",i);
        int k;
        for (k = 0; k < n;k++){
            printf("%d ", R[k]);
        }
        printf("\n");
    }
}
int main(void){
    int a[] = {5,6,7,8,9,4,3,2,1,0};
    bubble_sort1(a, 10);
}

输出结果

0: 0 5 6 7 8 9 4 3 2 1
1: 0 1 5 6 7 8 9 4 3 2
2: 0 1 2 5 6 7 8 9 4 3
3: 0 1 2 3 5 6 7 8 9 4
4: 0 1 2 3 4 5 6 7 8 9

算法分析

时间复杂度：

平均情况：比较复杂，但可以证明排序趟数为O(n),故时间复杂度为O(n^2^)
最坏情况：一开始元素就是有序从大到小的，每一次都需要交换，时间复杂度为 O(n^2^)
最好情况：一开始元素就是有序从小到大的，遍历一次即可，所以时间复杂度为O(n)

空间复杂度：

只使用了i，j，tmp三个辅助变量，与问题规模n无关。空间复杂度为O(1)

稳定性：

交换条件为R[j]<R[j-1]，故相同元素的相对位置不变。这是一种稳定的排序方法。

复杂性：

简单

归位：

全局有序。

本文由 ukuq 创作，采用知识共享署名4.0 国际许可协议进行许可
本站文章除注明转载/出处外，均为本站原创或翻译，转载前请务必署名
最后编辑时间为: Jan 25, 2019 at 10:43 pm