如何优雅地打印二叉树-2

书接上回，在如何优雅地打印二叉树中介绍了下打印二叉树的方法，但是并未给出二叉链的具体打印方法

调整核心：

用一个指针数组记录下相应节点位置，其中数组初始化为全0（空指针），其余部位依次根据读入数据修改。

另外，注意打印时判断指针是否为空，否则容易出现bug。

代码实现：

为了与第一篇对比，代码处仅进行了少量修改。具体应用时，还需要做出调整。

#include <stdio.h>
#include <stdlib.h>
#define MAXCOUNT 100
#define TREEARRAYCOUNT 10
const int BPOW[] = {0, 1, 3, 7, 15, 31, 63, 127};
typedef struct Node{
    char data;
    struct Node *l, *r;
}Node;

Node *nodeList[MAXCOUNT];//顺序存储二叉树
int nodeNum = 0;//记录二叉树数组的有效大小

void toList(Node * node,int n){
    if( node!=NULL){
        if(n>nodeNum)nodeNum = n;
        nodeList[n] = node;
        toList(node->l,2*n);
        toList(node->r, 2 * n + 1);
    }
}

void printBlank(int n){//打印n个空白单位
    for (int i = 0; i < n; i++)
        printf(" ");//按需调整“    ”
}

void printBinTree(Node * oldTree[],int s,int t){
    int nodeCount = t - s + 1;
    int MaxL = -1;
    Node **tree = oldTree + s;
    Node* treeArray[TREEARRAYCOUNT][TREEARRAYCOUNT] = {};
    for (int i = 0; i < nodeCount;){//分层
        MaxL++;
        for (int j = 0; j <= BPOW[MaxL] && i < nodeCount;)
            treeArray[MaxL][j++] = tree[i++];
    }
    MaxL++;//Better view
    for (int k = 0; k <= MaxL; k++){//打印
        printBlank(BPOW[MaxL - k]);
         //BPOW[k]+i<nodeCount，一个不多，一个不少↓
        for (int i = 0; i <= BPOW[k]&& (BPOW[k]+i<nodeCount); i++){
            if(treeArray[k][i]!=NULL){
                printf("%c", treeArray[k][i]->data);//按需调整“    ”
            }else
                printf("#");
            printBlank(BPOW[MaxL - k + 1]);
        }
        printf("\n");
    }
    printf("-----------------------------------\n");
}

Node* CreateTree(char* data,int i,int n){
    Node* bt = (Node*)malloc(sizeof(Node));
    bt->l = bt->r = NULL;
    bt->data = data[i];
    if(2*i<=n &&data[2*i]!=0)
        bt->l = CreateTree(data,2*i,n);
    if(2*i+1<=n &&data[2*i+1]!=0)
        bt->r = CreateTree(data,2*i+1,n);
    return bt;
}

int main(void){
    char tree[16] = {'0','1', '2', '3', '4', '5', '6', '7', '8', '9', 'A', 'B', 'C', 'D', 'E', 'F'};
    Node *root = CreateTree(tree, 1, 15);
    root->l->r = NULL;
    toList(root, 1);
    printBinTree(nodeList, 1, nodeNum);//有效数据从1开始
    return 0;
}

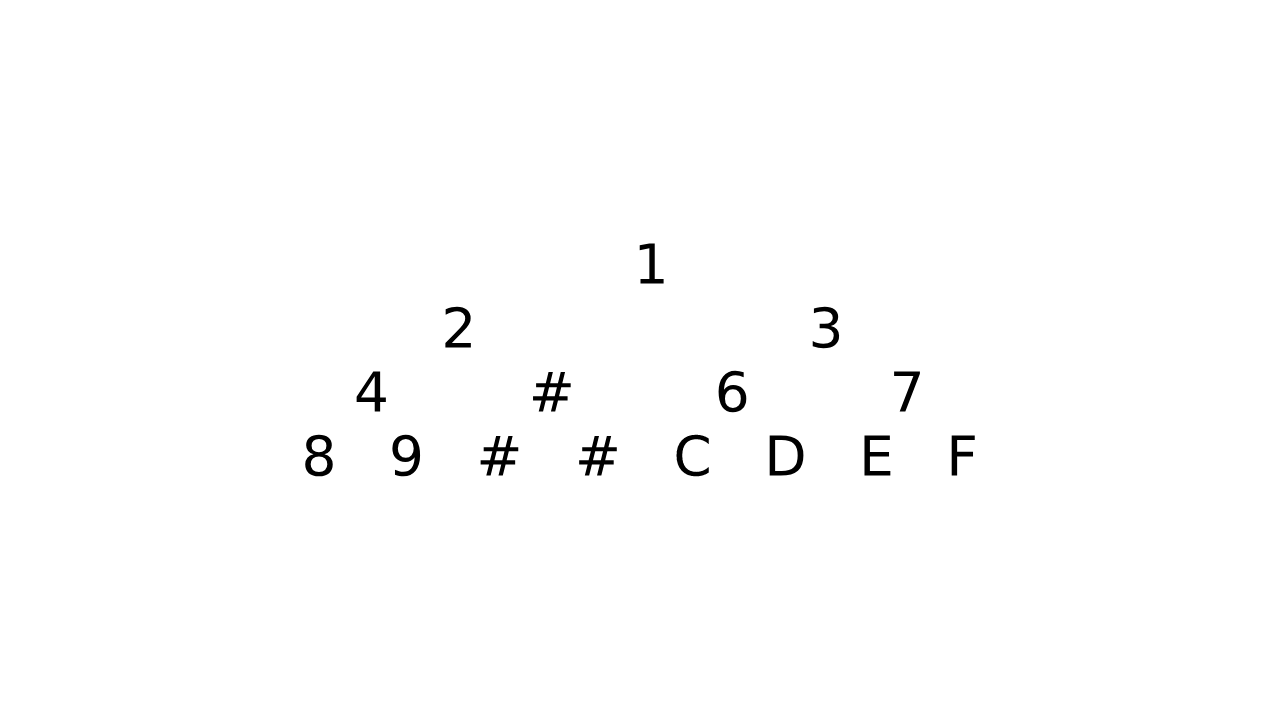
输出结果：

               1
       2               3
   4       #       6       7
 8   9   #   #   C   D   E   F

本文由 ukuq 创作，采用知识共享署名4.0 国际许可协议进行许可
本站文章除注明转载/出处外，均为本站原创或翻译，转载前请务必署名
最后编辑时间为: Mar 24, 2019 at 12:29 pm